 population.com.au
population.com.auLast official estimated population of Throsby (as Statistical Area Level 2) was 0 people (on 2017-06-30)[2]. This was 0.00% of total Australian population and 0% of ACT population. Area of Throsby is 1.50 km², in this year population density was 0.00 p/km² . If population growth rate would be same as in period 2016-2017 (0%/yr), Throsby population in 2025 would be 0. [0]
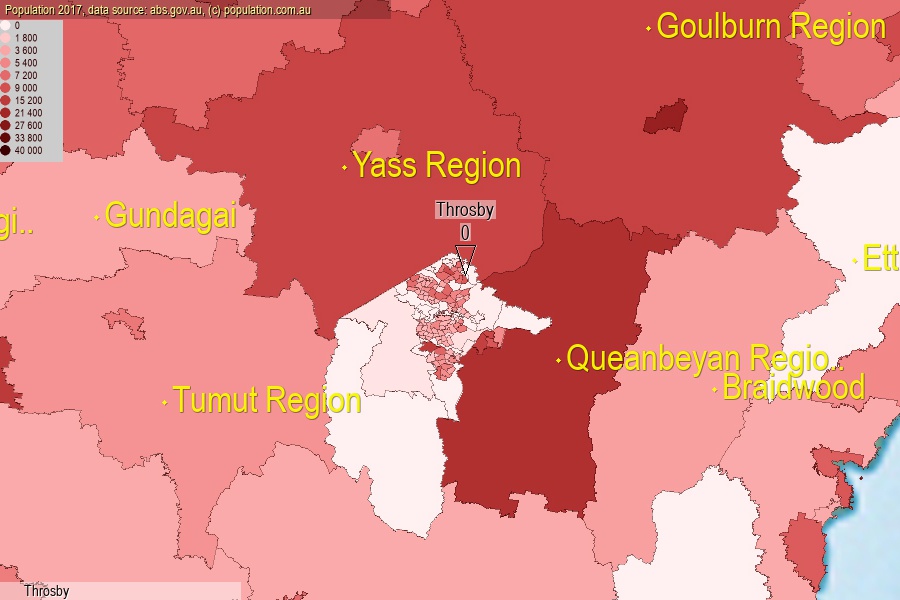
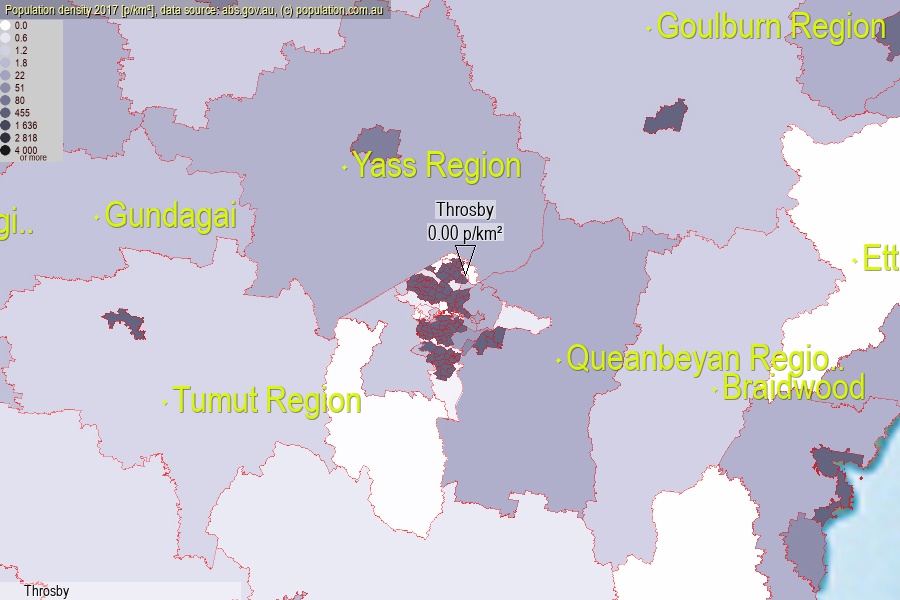
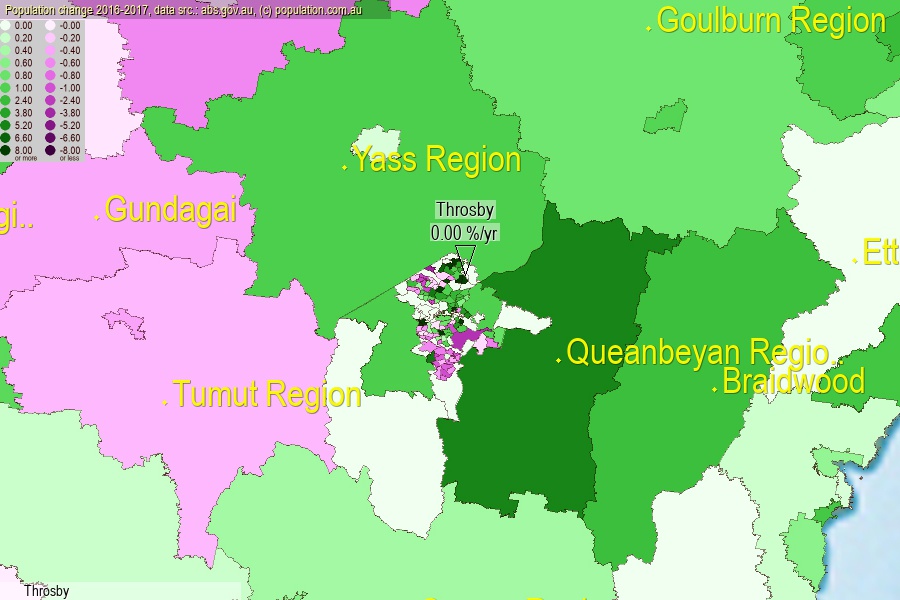
Click to enlarge. Throsby is located in the center of the images.
Population [people], population density [p./km²] and population change [%/year] [2]
View borders » (new window) [4]
[2001-2002] 0.00 %/Yr.
[2002-2003] 0.00 %/Yr.
[2003-2004] 0.00 %/Yr.
[2004-2005] 0.00 %/Yr.
[2005-2006] 0.00 %/Yr.
[2006-2007] 0.00 %/Yr.
[2007-2008] 0.00 %/Yr.
[2008-2009] 0.00 %/Yr.
[2009-2010] 0.00 %/Yr.
[2010-2011] 0.00 %/Yr.
[2011-2012] 0.00 %/Yr.
[2012-2013] 0.00 %/Yr.
[2013-2014] 0.00 %/Yr.
[2014-2015] 0.00 %/Yr.
[2015-2016] 0.00 %/Yr.
[2016-2017] 0.00 %/Yr.
[0] Calculated with linear interpolation from officially estimated population
[1] Read more about SA2 and Australian Statistical Geography Standard (ASGS) on abs.gov.au
[2] Population data from Australian Bureau of Statistics (Population and density: 2017; change: 2016-2017)
[3] Digital Boundaries: Australian Statistical Geography Standard (ASGS) 2016.
[4] Border coordinates are simplifyed using Ramer-Douglas-Peucker algorithm.